다익스트라(Dijkstra) 알고리즘
다익스트라 알고리즘은 다이나믹 프로그래밍을 활용한 대표적인 최단 경로 탐색 알고리즘이다. 인공위성 GPS 소프트웨어 등에서 가장 많이 사용되는 알고리즘이다.
다익스트라 알고리즘은 특정한 하나의 정점에서 다른 모든 정점으로 가는 최단 경로를 계산한다. 이때, 거리가 음수인 간선은 포함할 수 없다. 하지만, 현실 세계에서는 거리가 음수인 경로는 존재하지 않아서 다익스트라는 현실 세계에 적용하기 매우 적합한 알고리즘 중 하나이다.
다익스트라 알고리즘이 다이나믹 프로그래밍인 이유는 “최단 거리가 여러 개의 최단 거리”로 이루어져 있기 때문이다. 즉, 하나의 최단 거리를 구할 때, 이전까지 구했던 최단 거리 정보를 그대로 사용한다는 것이다.
작동 예시
다음과 같이 1번 노드에서 각 노드까지 최단 거리를 구한다고 해보자.
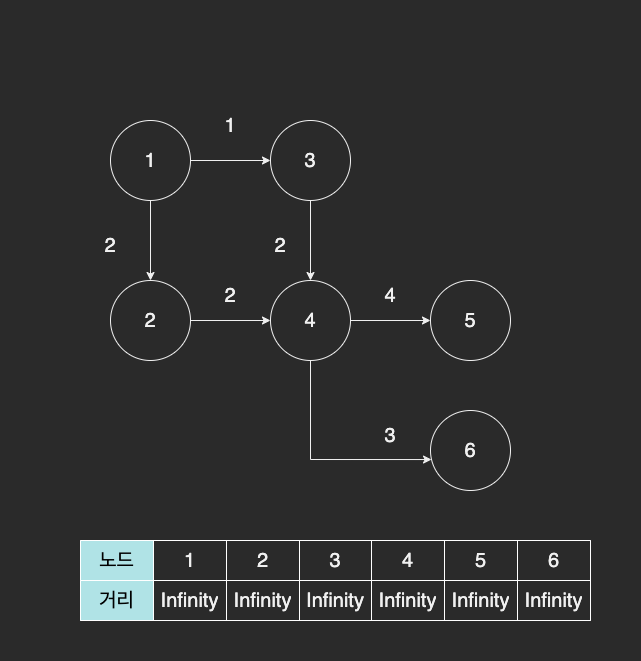
노드 간의 거리를 저장하는 테이블에는 무한대의 값을 저장해서 영원히 닿을 수 없다는 의미로 초기화 했다.
출발 노드는 1번 노드에서 시작한다. 1번 노드는 자기 스스로와 거리가 0 이기 때문에 먼저 0 으로 채워넣는다.
.png) )
)
현재 1번 노드와 직접 연결된 노드는 2, 3번 노드이다. 각각의 노드까지 걸리는 거리를 다음과 같이 테이블에 저장한다.
.png) )
)
이제 다음에 방문할 수 있는 노드는 2번과 3번 노드이다. 이 중에서 거리 테이블 상에서 가장 작은 값을 가진 3번 노드를 방문한다.
.png) )
)
3번 노드와 4번 노드의 거리는 2 인데, 거리 테이블의 4번 노드 자리에
- 1번 노드에서 3번 노드까지 이동한 거리
- 3번 노드에서 4번 노드까지 이동한 거리
를 더해서 저장한다. 즉, 1번 노드부터 누적해서 이동한 거리를 저장하는 것이다.
그 다음, 다시 거리 테이블에서 가장 작은 값을 가졌고, 방문하지 않은 노드인 2번 노드를 방문한다.
.png) )
)
2번 노드와 연결된 4번 노드까지 거리는 2이고, 2번 노드를 거쳐 4번 노드로 간다면 총 거리는 4가 된다. 하지만, 3번 노드를 거쳐서 간 거리가 훨씬 짧기 때문에 거리 테이블에서는 값을 갱신하지 않는다.
마찬가지로 이전과 동일하게 거리 테이블 상에서 가장 작은 값을 가지면서, 방문하지 않은 4번 노드를 방문한다.
.png) )
)
4번 노드부터 5번 노드와 6번 노드까지 거리를 기존에 이동한 거리와 더한 만큼 거리 테이블에 각각 저장한다.
다음으로, 거리 테이블 상에서 가장 작은 값을 가진 5번 노드를 방문한다.
.png) )
)
하지만 더 이상 이동할 경로가 없으므로 마지막 남은 6번 노드를 방문한다.
.png) )
)
이제 모든 노드를 방문했기 때문에 탐색을 멈춘다.
최종적으로 거리 테이블에 저장된 값들은 1번 노드에서 각각의 노드까지 최단 거리가 저장된 것이다. 즉, 3번 노드를 거쳐 가는 경로가 가장 최단 경로가 되는 것이다.
.png) )
)
특징
다익스트라 알고리즘은 방문하지 않은 노드 중, 최단 거리인 노드를 선택하는 과정을 반복한다. 그리고 선택한 노드는 다시 한번 최단 거리를 갱신하는데, 이후에는 더 이상 작은 값으로 갱신되지 않는다.
한편, 다익스트라 알고리즘은 거리가 양수일 때만 사용할 수 있다.
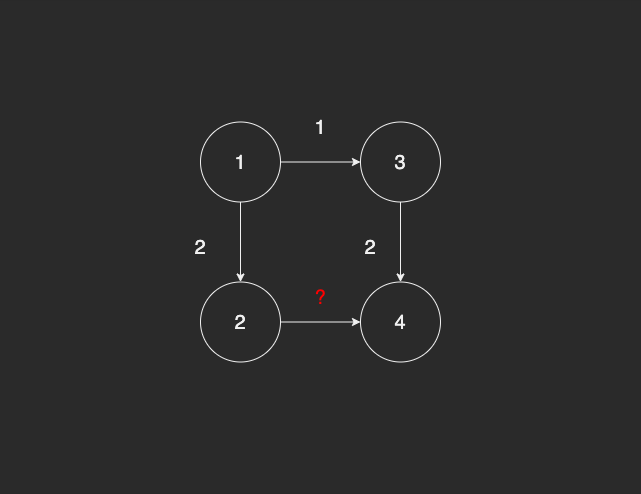
위와 같이 2번 노드에서 4번 노드로 가는 거리를 모른다고 해보자. 그렇다면, 1번 노드에서 4번 노드로 가는 최단 경로가 3번 노드를 거쳐야 하는 것이라는 것을 보장할 수 있을까?
만약, 2번 노드에서 4번 노드까지 거리가 0 이거나 음수이면 2번 노드를 거치는 것이 최단 경로가 될 것이다. 그렇기 때문에 1번 노드에서 3번 노드를 거쳐가는 경로가 최단 거리라고 할 수 없는 것이다.
구현하기 (JavaScript)
다익스트라 알고리즘은 BFS 를 기반으로 구현할 수 있다.
세부적으로는 크게 2가지로 구현할 수 있는데, 거리 테이블을 매번 탐색하는 ‘순차 탐색’ 방식과 거리가 짧은 노드를 우선 탐색하는 ‘우선순위 큐’를 이용한 방식이 있다.
아래와 같은 그래프에 대해 JavaScript 를 사용해서 구현했다.
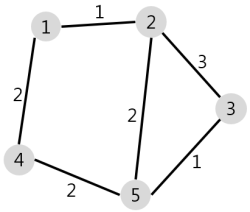
1. 순차 탐색
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
// 노드 간의 거리를 초기화
const graph = [
[Infinity, 1, Infinity, 2, Infinity],
[1, Infinity, 3, Infinity, 2],
[Infinity, 3, Infinity, Infinity, 1],
[2, Infinity, Infinity, Infinity, 2],
[Infinity, 2, 1, 2, Infinity],
];
// 방문 여부를 기록할 배열 생성
const visited = Array(N).fill(false);
// 1번 노드로부터 각 노드까지의 최단 거리를 저장한 배열 생성
const dist = visited.map((_, i) => graph[0][i]);
// 방문하지 않았으면서 거리 테이블에서 가장 작은 값을 가진 노드 탐색
const findSmallestNode = (visited, distance) => {
let minDist = Infinity;
let minIdx = 0;
for (let i = 0; i < distance.length; i++) {
if (visited[i]) continue;
if (distance[i] < minDist) {
minDist = distance[i];
minIdx = i;
}
}
return minIdx;
};
// 다익스트라 알고리즘 수행
const dijkstra = (graph, visited, dist) => {
// 1번 노드는 거리를 0으로 설정하고, 방문한 것으로 처리
distance[0] = 0;
visited[0] = true;
/*
현재 방문한 노드는 거리 테이블 상에서 가장 거리가 짧은 값을 가진 노드.
다음에 방문할 노드에 저장된 값이
"현재 방문한 노드까지 누적 이동 거리 + 다음 노드까지 거리"보다 크다면
"현재 방문한 노드까지 누적 이동 거리 + 다음 노드까지 거리"를 거리 테이블의 다음 방문할 노드에 저장
*/
for (let i = 0; i < distance.length; i++) {
const nodeIdx = findSmallestNode(visited, distance);
visited[nodeIdx] = true;
for (let j = 0; j < distance.length; j++) {
if (visited[j]) continue;
if (distance[j] > distance[nodeIdx] + graph[nodeIdx][j])
distance[j] = distance[nodeIdx] + graph[nodeIdx][j];
}
}
};
순차 탐색 방식은 ‘방문하지 않은 노드 중 거리값이 가장 작은 노드’를 다음 탐색 노드로 선택한다. 그 노드를 찾는 방식은 거리 테이블의 앞에서부터 찾아내야 하기 때문에 시간 복잡도는 $O(N^2)$ 이 된다.
시간 복잡도를 줄이기 위해 $O(log\ n)$ 을 보장하는 우선순위 큐를 사용한다.
다만, JavaScript 에서 우선순위 큐 자체를 구현하기 보다 우선순위 큐 개념을 이용해서 구현했다.
2. 우선순위 큐
그래프는 2차원 배열 안에 객체 형태로 to 목적지와 dist 거리를 저장했다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
// 0번 노드는 사용하지 않는 빈 노드이다.
// 이는 시작 노드를 1번으로 설정하기 위함이다.
const graph = [
[], // 사용X
[
{ to: 2, dist: 1 },
{ to: 4, dist: 2 },
],
[
{ to: 1, dist: 1 },
{ to: 3, dist: 3 },
{ to: 5, dist: 2 },
],
[
{ to: 2, dist: 3 },
{ to: 5, dist: 1 },
],
[
{ to: 1, dist: 2 },
{ to: 5, dist: 2 },
],
[
{ to: 2, dist: 2 },
{ to: 3, dist: 1 },
{ to: 4, dist: 2 },
],
];
// 1번 노드와 각 노드까지 최단 경로를 저장하는 배열 생성
const dist = Array(graph.length).fill(Infinity);
// 큐 생성 및 1번 노드에 대한 정보 저장
const queue = [{ to: 1, dist: 0 }];
// 1번 노드의 거리는 0 으로 설정
dist[1] = 0;
// 큐가 빌 때까지 반복
while (queue.length) {
// 큐에서 방문할 노드 꺼내기
const { to } = queue.pop();
// 방문한 노드까지 이동한 거리 + 다음 방문 노드까지 거리를
// 기존에 저장된 값과 비교해서 갱신
graph[to].forEach((next) => {
const acc = dist[to] + next.dist;
if (dist[next.to] > acc) {
dist[next.to] = acc;
// 최단 경로가 되는 노드는 큐에 추가
queue.push(next);
}
});
}
연습 문제
참고자료
- 다익스트라(Dijkstra) 알고리즘 [네이버 블로그]
- [알고리즘] 다익스트라(Dijkstra) 알고리즘 [velog]
- [ 다익스트라 알고리즘 ] 개념과 구현방법 (C++) [티스토리]
- [자료구조] 우선순위 큐 (Priority Queue) 개념 및 구현 [티스토리]
- [자료구조] 힙 (Heap) or 이진 힙(binary heap) [티스토리]
