TL; DR
- DFS 는 스택과 재귀를 이용한다.
- BFS 는 큐와 반복문을 이용한다.
- 문제에서 요구하는 조건에 따라 DFS 나 BFS 둘 중 하나를 선택한다.
미로찾기 알고리즘이란?

미로찾기 알고리즘은 코딩 테스트에서 자주 등장하는 알고리즘이다.
시작 지점과 도착 지점이 주어지며, 탈출할 수 있는 경로를 출력하거나 탈출까지 걸리는 최단 거리를 구할 수도 있다.
문제에 따라 DFS(Depth First Search)와 BFS(Breadth First Search) 를 적절하게 선택해서 해결할 수 있다.
적절한 지는 모르겠으나, 두 방식을 비유를 통해 비교한다면 다음과 같이 할 수 있을 것 같다.
컵 여러 개가 일렬로 있을 때, 컵에 물을 채우는 방식
- DFS : 맨 앞의 컵에만 계속 물을 붓고, 넘치는 물로 다음 컵을 채우기
- BFS : 물뿌리개로 동시에 여러 컵을 채우기
DFS (Depth First Search)
DFS 는 모든 노드를 방문하는 경우에 사용한다.
주로 스택과 재귀 함수를 활용한다.
재귀 함수를 사용하는 경우에는 종료 조건을 명확하게 명시해야 하며, 그렇지 않으면 무한 반복에 빠진다.
📌 백트래킹(backtracking)
DFS 를 활용할 때는 백트래킹(backtracking) 알고리즘을 사용한다.
백트래킹이란 해를 찾아가는 도중, 지금 가는 경로가 해가 아니라면 더 이상 경로를 가지 않고 되돌아가는 것을 의미한다. 백트래킹의 목적은 불필요한 탐색을 줄이고, 최대한 올바른 쪽으로 가고자 하는 것이다.
즉, 모든 가능한 경우의 수 중에서 특정한 조건을 만족하는 경우만 살펴보는 것이다.
백트래킹을 사용해서 풀 수 있는 대표적인 문제로는 N-Queen 문제가 있다.
🗺 미로 탈출 지점 찾기
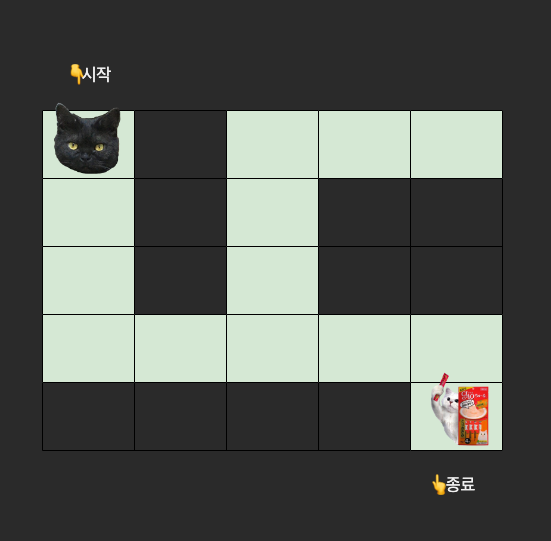
(0, 0) 좌표에 귀여운 고양이 한 마리가 있다. 이 고양이는 (4, 4) 좌표에 있는 츄르를 먹기 위해 미로를 따라 이동한다.
이때, 귀여운 고양이가 미로를 탐색하는 방법은 다음과 같다.
- 상하좌우를 살피며 이동할 수 있는 지 확인
- 이동할 수 있으면 해당 공간으로 이동
- 1 ~ 2 을 반복하다가 더 이상 나아갈 수 없으면 해당 경로에서 빠져나온다.
- 1 ~ 3 의 과정을 반복하며 탈출구를 찾는다.
처음 3번에 해당하는 순간은 다음과 같을 것이다.
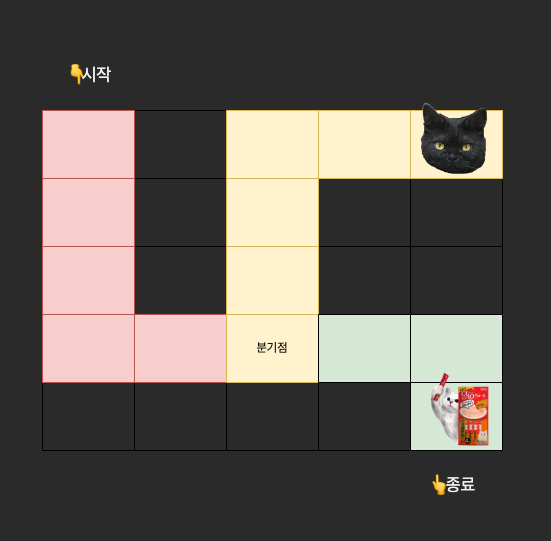
(2, 3) 좌표에서 오른쪽으로도 갈 수 있었지만, 위쪽을 먼저 탐색한다는 조건이 있었기에 (2, 2) 좌표로 이동하여 해당 경로의 끝까지 이동한다.
그리고 벽에 부딪힌 순간에는 다시 분기점으로 돌아서 나오고, 이동이 가능한 (3, 3) 방향으로 다시 진행한다.

위의 과정을 의사 코드로 구현하면 다음과 같다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
const offset =
[
[0, 1], // 상
[0, -1], // 하
[-1, 0] // 좌
[1, 0] // 우
]
void find_path(maps, visited, pos)
{
if (pos == [4, 4]) // 종료 조건
return ;
else
{
visited[pos] = true; // 현재 위치를 방문한 것으로 표시
stack.push(pos); // 현재 위치를 스택에 넣기
for (i = 0; i < 4; i++) // 상하좌우 이동 여부 탐색
{
next = pos + offset[i]; // 다음 좌표 저장
if (is_movable(maps, next) // 이동 가능 여부 판단
find_path(maps, visited, next); // 다음 경로로 이동
}
stack.pop(pos); // 탐색에 실패하면 스택에서 현재 위치 제거
}
}
실제로 움직인다면 다음과 같이 움직일 것이다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
[0, 0] -> 시작 지점
[0, 1]
[0, 2]
[0, 3]
[1, 3]
[2, 3] -> 분기 지점
[2, 2] -> 위로 이동
[2, 1]
[2, 0]
[3, 0]
[4, 0] -> 벽에 부딪히는 순간 뒤로 이동
[3, 0]
[2, 0]
[2, 1]
[2, 2]
[2, 3] -> 분기 지점
[3, 3] -> 오른쪽으로 이동
[4, 3]
[4, 4] -> 종료 지점
(4, 0) 에 도달한 시점에는 스택에는 다음과 같이 저장된다.
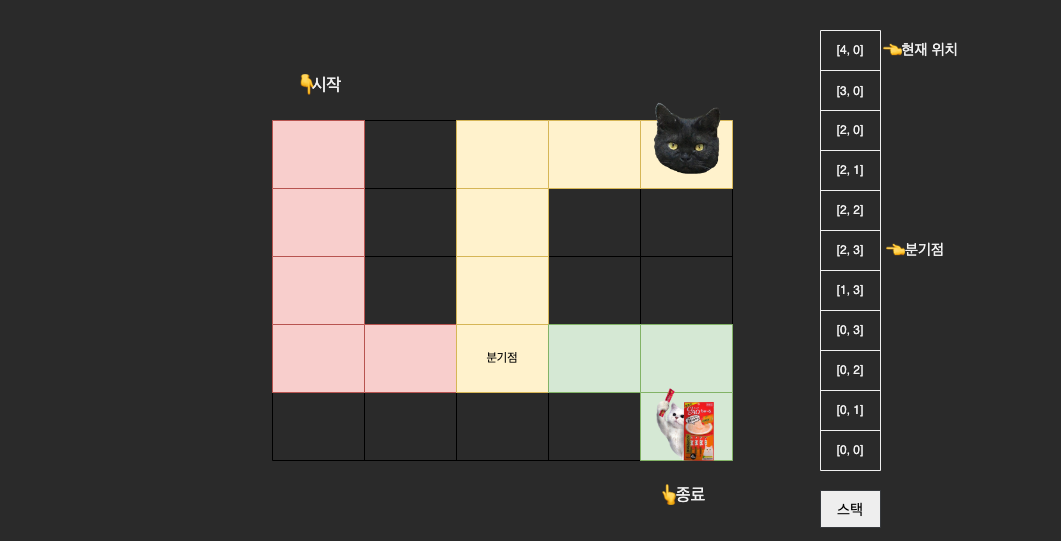
다시 돌아나갈 때는 분기점까지 쌓은 스택을 모두 빼내면 된다. 그리고 도착 지점에 도착했을 때는 스택에 다음과 같이 저장된다.
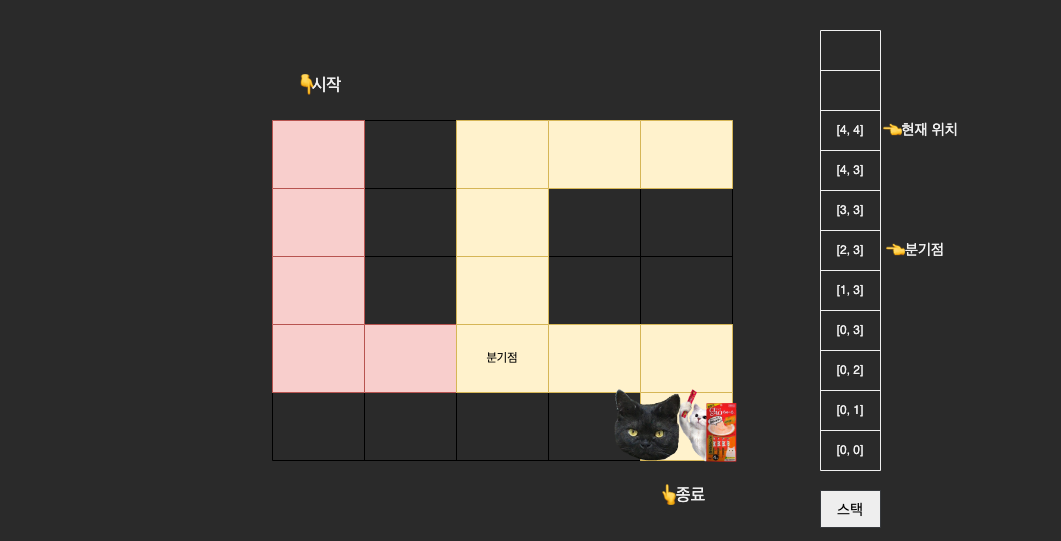
✍️ 코드로 구현하기
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
// 변수 선언
int NUM_DIRECTIONS = 4;
static int DIRECTION_OFFSETS[NUM_DIRECTIONS][2] = {
{0, -1}, // 0 (상)
{1, 0}, // 1 (우)
{0, 1}, // 2 (하)
{-1, 0} // 3 (좌)
};
struct MapPositionType
{
int x;
int y;
int direction;
} MapPosition;
enum PosStatus { NOT_VISIT = 0, WALL = 1 , VISIT = 2 };
// 재귀 함수
int findPath(int maze[HEIGHT][WIDTH], MapPosition pos, LinkedStack *pStack)
{
MapPosition nextPos;
int nextX;
int nextY;
if (!pStack)
return (ERROR);
// 현재 위치가 미로의 범위를 벗어나는 지 확인
if (pos.x < 0 || pos.y < 0 || pos.x >= WIDTH || pos.y >= HEIGHT)
return (FALSE);
// 현재 위치가 벽이거나 이미 방문한 곳인지 확인
else if (maze[pos.y][pos.x] == WALL || maze[pos.y][pos.x] == VISIT)
return (FALSE);
// 도착 지점에 도달한 경우
else if (maze[pos.y][pos.x] == END)
{
pushLS(pStack, pos);
return (TRUE);
}
// 백트래킹을 통한 탐색 반복
else
{
pushLS(pStack, pos); // 현재 위치를 스택에 저장
maze[pos.y][pos.x] = VISIT; // 현재 위치를 2로 변경
while (pos.direction < NUM_DIRECTIONS)
{
// 다음 좌표 설정
nextX = pos.x + DIRECTION_OFFSETS[pos.direction][0];
nextY = pos.y + DIRECTION_OFFSETS[pos.direction][1];
nextPos.x = nextX;
nextPos.y = nextY;
nextPos.direction = 0;
if (findPath(maze, nextPos, pStack))
return (TRUE);
pos.direction += 1;
}
// 길을 찾지 못하면 스택에서 현재 위치 제거
popLS(pStack);
return (FALSE);
}
}
🤔 DFS 의 한계?
DFS 는 크게 2가지 단점이 존재한다.
1. 연산 횟수의 기하급수적인 증가
DFS 는 모든 가능한 경우의 수를 탐색하기 때문에 미로의 크기가 커질 경우, 연산이 기하급수적으로 늘어나기 때문에 실행 시간도 같이 증가하는 문제점이 있다.
예를 들어, 다음과 같은 미로가 있다고 해보자.
| 1 🏃♂️ | 1 | 1 | 1 | 1 | 1 | 1 | ||||
| 1 | 1 | 1 | 1 | 1 | ||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | ||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 👑 |
첫 번째 갈림길인 (3, 3) 지점에서 선택할 수 있는 경로의 수는 3가지다. 그리고 두 번째 갈림길인 (7, 3) 에서도 선택할 수 있는 경로의 수는 3가지다. 따라서 갈림길에서 선택할 수 있는 모든 경우의 수는 $3^2 = 9$ 이다. 만약, 갈림길이 2개가 아니라 1000 개면 경로의 수는 $3^{1000}$ 이 될 것이다.
2. 최단 거리 보장 🙅♂️
DFS 는 최단 거리를 보장하지 못한다.
예를 들어, 다음과 같은 미로가 있다고 해보자. 이때, 해를 찾으면 다른 유망한 경로는 찾지 않고 바로 종료한다고 가정한다.
| 1 🏃♂️ | 1 | 1 | 1 | |
| 1 | 1 | 1 | ||
| 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 👑 |
탐색하는 순서가 상 - 우 - 하 - 좌 순이라면, 다음과 같이 탐색할 것이다.
| 1 🏃♂️ | 1 | 1 | 1 | |
| 2 🏃♂️ | 1 | 1 | ||
| 3 🏃♂️ | 7 🏃♂️ | 8 🏃♂️ | 9 🏃♂️ | |
| 4 🏃♂️ | 5 🏃♂️ | 6 🏃♂️ | 10 🏃♂️ | |
| 1 | 1 | 11 🏃♂️ |
만약, 탐색하는 순서가 하 - 우 - 상 - 좌 순이라면, 다음과 같이 탐색할 것이다.
| 1 🏃♂️ | 1 | 1 | 1 | |
| 2 🏃♂️ | 1 | 1 | ||
| 3 🏃♂️ | 1 | 1 | 1 | |
| 4 🏃♂️ | 5 🏃♂️ | 6 🏃♂️ | 1 | |
| 7 🏃♂️ | 8 🏃♂️ | 9 🏃♂️ |
이를 통해 DFS 는 탐색하는 순서에 따라 해가 바뀔 수 있으며, 발견한 해가 반드시 최적해가 아니라는 것을 알 수 있다.
따라서 최단 거리를 찾기 위해서는 DFS 보다는 BFS 를 사용한다.
BFS (Breadth First Search)
BFS 는 같은 레벨을 우선적으로 탐색하는 알고리즘이다.
보통 큐와 반복문을 사용하며, 노드 사이의 최단 경로를 찾을 때 사용한다.
🏃♂️ 최단 거리 찾기
미로가 다음과 같다고 해보자.
| 1 🏃♂️ | 1 | 1 | 1 | |
| 1 | 1 | 1 | ||
| 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | |
| 1 | 1 | 1 👑 |
처음 분기가 시작되는 지점은 (2, 3) 인데, BFS 는 다음과 같이 진행한다. (💦 : 분기)
| 1 🏃♂️ | 3️⃣ 9 | 4️⃣ 10 | 5️⃣ 11 | |
| 2 🏃♂️ | 2️⃣ 8 | 4️⃣ 10 | ||
| 3 🏃♂️ | 1️⃣ 7 💦 | 2️⃣8 | 3️⃣ 9 💦 | |
| 4 🏃♂️ | 5 🏃♂️ | 6 💦 | 4️⃣ 10 | |
| 1️⃣ 7 | 2️⃣ 8 | 3️⃣ 9 👑 |
분기점에서 하나의 경로를 계속 따라가는 것이 아니라 슬라임이 퍼져나가듯이 동시에 여러 경로를 탐색하는 것이다.
저장되는 값은 현재까지 이동한 거리를 의미하며, 숫자 이모지는 동시에 이동한 것을 표시한 것이다.
의사 코드로 구현하면 다음과 같다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void bfs(maps, start, visited)
{
queue.enqueue([start]); // 시작 지점을 큐에 넣기
while (!queue.isEmpty()) // 큐가 비워지기 전까지 반복
{
now = queue.dequeue(); // 큐에서 꺼내기
if (now == [end]) // 종료 지점에 도달한 경우
return ;
visited[now] = true; // 현재 위치를 방문 처리
for (int i = 0; i < 4; i++)
{
next = now + offset[i]; // 다음 방문 좌표 생성
if (is_movable(maps, next, visited)) // 이동 가능 여부 확인
queue.enqueue(next); // 큐에 다음 방문 좌표 넣기
}
}
}
✍️ 코드로 구현하기
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
// 변수 선언은 이전 예제와 동일
int is_movable(int maze[HEIGHT][WIDHT], int visited[HEIGTH][WIDTH], MapPosition pos)
{
// 현재 위치가 미로의 범위를 벗어나는 지 확인
if (pos.x < 0 || pos.y < 0 || pos.x >= WIDTH || pos.y >= HEIGHT)
return (FALSE);
// 현재 위치가 벽이거나 이미 방문한 곳인지 확인
if (maze[pos.y][pos.x] == WALL || maze[pos.y][pos.x] == VISIT)
return (FALSE);
return (TRUE);
}
// BFS
int findPath(int maze[HEIGHT][WIDTH], int visited[HEIGHT][WIDTH], MapPosition pos)
{
LinkedQueue queue;
MapPosition currPos;
MapPosition nextPos;
int nextX;
int nextY;
queue.enqueue(pos); // 처음 시작 위치를 큐에 넣기
while (!queue.isEmpty())
{
currPos = queue.dequeue(); // 큐에서 꺼내기
if (maze[currPos.y][currPos.x] == END) // 도착 지점에 도달한 경우
return (maze[currPos.y][currPos.x]);
if (visited[currPos.y][currPos.x] == VISIT) // 현재 위치를 방문했는지 확인
continue ;
visited[currPos.y][currPos.x] = VISIT; // 현재 위치를 VISIT 으로 변경
while (currPos.direction < NUM_DIRECTIONS)
{
// 다음 좌표 설정
nextX = currPos.x + DIRECTION_OFFSETS[currPos.direction][0];
nextY = currPos.y + DIRECTION_OFFSETS[currPos.direction][1];
nextPos.x = nextX;
nextPos.y = nextY;
nextPos.direction = 0;
if (is_movable(maze, visited, nextPos)
{
// 다음 이동 지점에 이전 이동 거리 + 1 저장
maze[nextY][nextX] = maze[currPos.y][currPos.x] + 1;
queue.enqueue(nextPos); // 다음 이동 지점 큐에 저장
}
pos.direction += 1;
}
}
}
🤔 BFS 의 한계?
1. DFS 에 비해 큰 저장공간이 필요
DFS 와 달리 다음 탐색할 노드를 동시에 여러 개 저장하기 때문에 갈림길이 많을 수록 유망하지 않은 노드까지 저장해야 한다.
2. 규모가 클 경우 비효율적
DFS 는 규모가 크더라도 최선의 경우에는 어떤 경로 하나에서만 도착하기만 하면 종료한다. 하지만, BFS 는 동시에 여러 경로를 탐색해야 하기 때문에 프로그램 실행 시간이 오래 걸린다는 단점이 있다.
DFS, BFS 정리
두 알고리즘 모두 장단점이 있기 때문에 상황에 맞춰서 선택하면 된다.
DFS
- 모든 경우의 수를 구해야 하는 경우
- 검색 대상의 규모가 큰 경우
BFS
- 최단 거리를 구해야 하는 경우
- 검색 대상의 규모가 작고, 검색 시작 지점으로부터 원하는 대상이 멀지 않은 경우
연습 문제
- 프로그래머스 - 게임 맵 찾기
- 프로그래머스 - 방문 길이
- 프로그래머스 - 모음 사전
- 프로그래머스 - 피로도
- 프로그래머스 - 타겟 넘버
- 프로그래머스 - 메뉴 리뉴얼
- 프로그래머스 - 소수 찾기
- 프로그래머스 - 소수 만들기
참고자료
- 순환함수 (재귀함수) - JAVA 로 미로찾기 문제 구현 [티스토리]
- [Recursion]재귀: 미로찾기 C# [티스토리]
- DFS/BFS - 백트래킹/최단경로 [github.io]
- 조합 Combination (Java) [티스토리]
- 알고리즘 - 백트래킹(Backtracking)의 정의 및 예시문제 [github.io]
