문제 설명
문제 설명 생략
🙋♂️나의 풀이
🤔문제 접근
처음에는 DFS 로 접근해서 모든 경우의 수를 탐색해서 풀었다.
모든 경우의 수를 구하기 위해서 1차원 배열을 사용하는 방법을 먼저 떠올렸다.
- 가로가 1 인 직사각형은
1, 가로가 2 인 직사각형은2로 저장한다. n = 2일 때,[1, 1],[2]와 같이 저장할 수 있다.- 모든 경우의 수를 배열에 담아서 길이를 반환한다.
하지만 배열에 담는 것보다 Number 자료형의 값을 1씩 증가하는 것이 메모리를 덜 사용하는 방법이라 생각했다.
- 가로의 길이를 0 부터 시작해서 1과 2씩 증가시켰을 때,
n과 동일하다면Number자료형의 값을 1 증가 시킨다.
n 이 작을 때는 정답을 구했지만, n 의 최댓값이 60,000 이기 때문에 값이 커지면서 시간 복잡도가 증가하고, 시간 초과와 함께 콜 스택에 터지는 오류가 발생했다.
❌ 실패한 코드 (DFS)
1
2
3
4
5
6
7
8
9
10
11
12
function solution(n) {
let result = 0;
const dfs = (n, width) => {
if (n === width) {
result += 1;
return;
}
for (let i = 1; i <= 2; i++) if (width + i <= n) dfs(n, width + i);
};
dfs(n, 0);
return result;
}
다른 분들의 풀이를 참고하며 동적 계획법(Dynamic Programming)으로 접근하는 것을 알게 되었다.
동적 계획법에 대한 내용은 해당 링크에서 확인할 수 있다.
✅ 개념 적용하기
놓을 수 있는 직사각형의 가로 길이는 1 또는 2 이다.
전체 가로 길이를 n 이라 해보자.
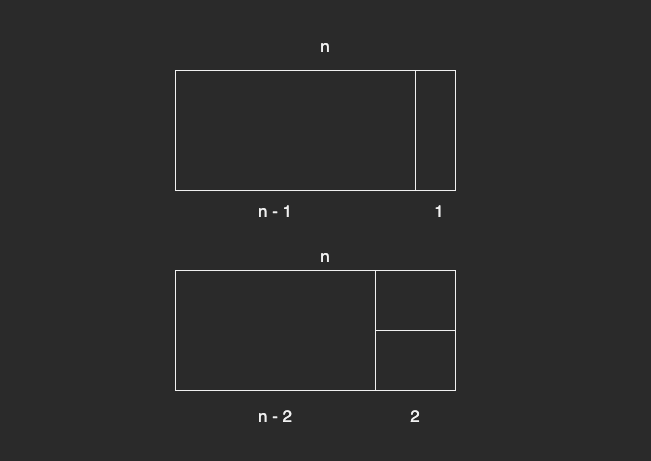
마지막에 놓는 타일은 가로가 1인 직사각형을 1개 배치하거나, 가로가 2인 직사각형을 2개 배치하는 방법이 있다. 그래서 가로의 길이가 n 인 직사각형을 만들기 위해서는 가로가 n - 1 인 직사각형을 만드는 경우의 수와 n - 2 인 직사각형을 만드는 경우의 수를 더한 것과 동일하다.
그렇다면 가로가 n - 1 인 직사각형을 채우는 경우의 수는 가로가 n - 2 인 직사각형을 채우는 경우의 수와 n - 3 인 직사각형을 채우는 경우의 수를 더한 것과 같다.
.png)
즉, $D[n] = D[n - 1] + D[n - 2]$ 관계가 성립한다는 것이다.
✍️ 작성 코드
Bottom-Up 방식
1
2
3
4
5
6
7
8
9
function solution(n) {
if (n === 1 || n === 2) return n;
const dp = Array(n).fill(0);
const mod = 1000000007;
dp[0] = 1;
dp[1] = 2;
for (let i = 2; i < n; i++) dp[i] = (dp[i - 1] + dp[i - 2]) % mod;
return dp[n - 1];
}
연산 결과를 저장할 1차원 배열 dp 의 길이를 n 으로 설정하고, 0 으로 초기화 한다.
그리고 n = 1 일 때 경우의 수인 1 과 n = 2 일 때 경우의 수인 2 를 배열의 가장 처음에 설정한다.
그 다음, 반복문을 돌며 점화식에 따라 연산을 수행한다.
참고로 연산 결과에 1000000007 로 나눈 나머지를 저장하는 이유는 경우의 수가 지나치게 많아지면 오버 플로우가 발생하기 때문이다. 그래서 오버 플로우가 발생하면 소수 1000000007 로 나눈 값을 결과로 받아서 처리하는 것이다.
Top-Down 방식
1
2
3
4
5
6
7
8
9
10
11
12
13
function solution(n) {
if (n === 1 || n === 2) return n;
const memo = Array(n + 1).fill(0);
const mod = 1000000007;
const dp = (n) => {
if (n <= 2) return n;
if (memo[n] > 0) return memo[n];
memo[n] = (dp(n - 1) + dp(n - 2)) % mod;
return memo[n];
};
return dp(n);
}
재귀 함수를 사용해서 구현한 코드이다. 정확성 테스트는 전부 맞지만, 효율성 테스트에서 실패한다. 이는 JavaScript 가 Call Stack 의 최대 개수를 제한하는 언어이기 때문이다.
실제로 n = 60000 일때, JavaScript 로 실행하면 Maximum call stack size exceeded 오류가 발생한다.
그렇기 때문에 JavaScript 로 구현한다면 Bottom-Up 방식으로 구현하는 것이 좋다.
