문제 설명
XX게임에는 피로도 시스템(0 이상의 정수로 표현합니다)이 있으며, 일정 피로도를 사용해서 던전을 탐험할 수 있습니다. 이때, 각 던전마다 탐험을 시작하기 위해 필요한 “최소 필요 피로도”와 던전 탐험을 마쳤을 때 소모되는 “소모 피로도”가 있습니다. “최소 필요 피로도”는 해당 던전을 탐험하기 위해 가지고 있어야 하는 최소한의 피로도를 나타내며, “소모 피로도”는 던전을 탐험한 후 소모되는 피로도를 나타냅니다. 예를 들어 “최소 필요 피로도”가 80, “소모 피로도”가 20인 던전을 탐험하기 위해서는 유저의 현재 남은 피로도는 80 이상 이어야 하며, 던전을 탐험한 후에는 피로도 20이 소모됩니다.
이 게임에는 하루에 한 번씩 탐험할 수 있는 던전이 여러개 있는데, 한 유저가 오늘 이 던전들을 최대한 많이 탐험하려 합니다. 유저의 현재 피로도 k와 각 던전별 “최소 필요 피로도”, “소모 피로도”가 담긴 2차원 배열 dungeons 가 매개변수로 주어질 때, 유저가 탐험할수 있는 최대 던전 수를 return 하도록 solution 함수를 완성해주세요.
제한사항
- k는 1 이상 5,000 이하인 자연수입니다.
- dungeons의 세로(행) 길이(즉, 던전의 개수)는 1 이상 8 이하입니다.
- dungeons의 가로(열) 길이는 2 입니다.
- dungeons의 각 행은 각 던전의 [“최소 필요 피로도”, “소모 피로도”] 입니다.
- “최소 필요 피로도”는 항상 “소모 피로도”보다 크거나 같습니다.
- “최소 필요 피로도”와 “소모 피로도”는 1 이상 1,000 이하인 자연수입니다.
- 서로 다른 던전의 [“최소 필요 피로도”, “소모 피로도”]가 서로 같을 수 있습니다.
🙋♂️나의 풀이
🤔문제 접근
- 던전에 입장할 수 있는 모든 경우의 수를 구한다. (순열)
- 모든 경우의 수에 대해 던전을 입장한 횟수를 1차원 배열에 저장한다.
- 2에서 구한 배열 요소 중에서 최댓값을 반환한다.
✍️작성 코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
function solution(k, dungeons) {
const permutations = getPermutations(dungeons, dungeons.length);
const dungeonEntranceCounts = countDungeonEntranceCount(k, permutations);
return Math.max(...dungeonEntranceCounts);
}
const getPermutations = (arr, selectNumber) => {
const result = [];
if (selectNumber === 1) return arr.map((el) => [el]);
arr.forEach((fixed, index, origin) => {
const rest = [...origin.slice(0, index), ...origin.slice(index + 1)];
const permutations = getPermutations(rest, selectNumber - 1);
const attached = permutations.map((permutation) => [fixed, ...permutation]);
result.push(...attached);
});
return result;
};
const countDungeonEntranceCount = (k, permutations) => {
return permutations.map((permutation) => {
let remain = k;
let count = 0;
permutation.forEach(([need, use]) => {
if (remain >= need) {
remain -= use;
count += 1;
}
});
return count;
});
};
던전에 입장할 수 있는 모든 순열을 getPermutations 함수를 사용해서 구한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
const permutations = getPermutations(dungeons, dungeons.length);
const getPermutations = (arr, selectNumber) => {
const result = [];
if (selectNumber === 1) return arr.map((el) => [el]);
arr.forEach((fixed, index, origin) => {
const rest = [...origin.slice(0, index), ...origin.slice(index + 1)];
const permutations = getPermutations(rest, selectNumber - 1);
const attached = permutations.map((permutation) => [fixed, ...permutation]);
result.push(...attached);
});
return result;
};
permutations 에 저장되는 값은 [[80, 20], [50, 40], [30, 10]] 을 기준으로 다음과 같다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
[
[
[80, 20],
[50, 40],
[30, 10],
],
[
[80, 20],
[30, 10],
[50, 40],
],
[
[50, 40],
[80, 20],
[30, 10],
],
[
[50, 40],
[30, 10],
[80, 20],
],
[
[30, 10],
[80, 20],
[50, 40],
],
[
[30, 10],
[50, 40],
[80, 20],
],
];
던전에 입장한 횟수를 구하기 위해 countDungeonEntraceCount 함수를 이용했다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
const dungeonEntranceCounts = countDungeonEntranceCount(k, permutations);
const countDungeonEntranceCount = (k, permutations) => {
return permutations.map((permutation) => {
let remain = k;
let count = 0;
permutation.forEach(([need, use]) => {
if (remain >= need) {
remain -= use;
count += 1;
}
});
return count;
});
};
경우의 수마다 피로도를 매번 remain 변수에 k 로 초기화 했다.
그 다음 던전 입장에 필요한 피로도 need 보다 remain 이 많으면 소모되는 피로도 use 만큼 remain 에서 감소시켰다. 그리고 던전 입장 횟수를 저장하는 count 변수를 1 만큼 증가시켰다.
dungeonEntranceCounts 에 저장되는 값은 다음과 같다.
1
[2, 3, 2, 2, 2, 2];
마지막으로 최댓값을 반환하면 되므로 다음과 같이 리턴해주었다.
1
return Math.max(...dungeonEntranceCounts);
채점 결과는 다음과 같다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
테스트 1 〉 통과 (0.31ms, 30.2MB)
테스트 2 〉 통과 (0.29ms, 29.9MB)
테스트 3 〉 통과 (0.62ms, 30.2MB)
테스트 4 〉 통과 (0.62ms, 30MB)
테스트 5 〉 통과 (7.87ms, 34.3MB)
테스트 6 〉 통과 (25.85ms, 41.6MB)
테스트 7 〉 통과 (84.51ms, 60.3MB)
테스트 8 〉 통과 (96.11ms, 60.5MB)
테스트 9 〉 통과 (0.64ms, 30.2MB)
테스트 10 〉 통과 (18.12ms, 42.5MB)
테스트 11 〉 통과 (0.28ms, 30.3MB)
테스트 12 〉 통과 (85.97ms, 59.7MB)
테스트 13 〉 통과 (111.97ms, 59.6MB)
테스트 14 〉 통과 (111.69ms, 60.4MB)
테스트 15 〉 통과 (105.41ms, 60.3MB)
테스트 16 〉 통과 (19.56ms, 42MB)
테스트 17 〉 통과 (98.97ms, 61.3MB)
테스트 18 〉 통과 (0.32ms, 30MB)
테스트 19 〉 통과 (1.15ms, 30.1MB)
⚙️ 리팩토링
위의 코드에서는 순열을 만들 때는 재귀함수를 사용하고, 모든 경우의 수를 순회할 때는 반복을 2번 사용하기 때문에 $O(n^2)$ 보다 더 큰 시간 복잡도를 갖는다.
따라서 반복을 최대한 줄여서 구하는 코드를 다른 분들의 코드를 참고해서 리팩토링 해보았다.
✍️ 작성 코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
function solution(k, dungeons) {
const answer = dfs(0, k, dungeons, new Set());
return Math.max(...answer);
}
const dfs = (count, tired, dungeons, result) => {
result.add(count); // 아무 던전도 입장하지 못하고 나올 때는 0 을 저장
dungeons.forEach((dungeon, i) => {
const [need, use] = dungeon;
if (tired >= need) {
const next = [...dungeons.slice(0, i), ...dungeons.slice(i + 1)];
dfs(count + 1, tired - use, next, result);
}
});
return [...result];
};
최종적으로 반환하는 answer 변수에는 Set 자료형이 저장된다. Set 를 사용하는 이유는 동일한 횟수만큼 입장한 경우에 대해 중복을 제거하기 위해서다.
1
const answer = dfs(0, k, dungeons, new Set());
예를 들어, 5가지 경우의 수에 대해서 1차원 배열에 입장 횟수를 [1, 2, 2, 3, 2] 과 같이 저장한다고 했을 때, 최댓값인 3이 아닌 다른 값들은 중복될 필요가 없기 때문이다.
따라서 answer 변수에는 (0, 1, 2, 3) 과 같이 중복이 제거된 값만 저장했다.
dfs 함수는 던전을 모두 순회하며 던전 입장 횟수를 구하도록 재귀적으로 구현했다. 그림으로 나타내면 다음과 같다.
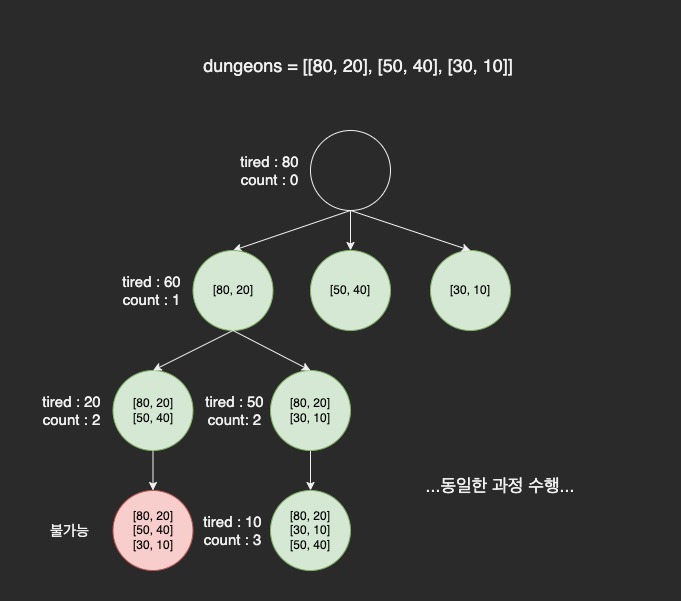
백트래킹을 통해 유망하지 않은 경우는 더 이상 탐색하지 않는다. (빨간색 원)
next 변수에는 현재 입장한 던전을 제외한 나머지 던전을 저장했다.
1
const next = [...dungeons.slice(0, i), ...dungeons.slice(i + 1)];
위의 그림에서 dfs 함수 내부의 변수에 저장되는 값을 정리하면 다음과 같다.
| 재귀 레벨 | count | tired | dungeons | result | dungeon | next |
|---|---|---|---|---|---|---|
| 0 | 0 | 80 | [[80, 20], [50, 40], [30, 10]] | (0) | [80, 20] | [[50, 40], [30, 10]] |
| 1 | 1 | 60 | [[50, 40], [30, 10]] | (0, 1) | [50, 40] | [[30, 10]] |
| 2 | 2 | 20 | [[30, 10]] | (0, 1, 2) | [30, 10] | 탐험 불가 |
| 1 | 1 | 60 | [[50, 40], [30, 10]] | (0, 1) | [30, 10] | [[50, 40]] |
| 2 | 2 | 50 | [[50, 40]] | (0, 1, 2) | [50, 40] | [[]] |
| 3 | 3 | 10 | [[]] | (0, 1, 2, 3) | [] | 탐험 끝 |
dfs 로 구현한 코드는 코드도 간결해졌고, 실행 속도도 훨씬 빨라졌다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
// DFS
테스트 1 〉 통과 (0.17ms, 30.1MB)
테스트 2 〉 통과 (0.19ms, 30MB)
테스트 3 〉 통과 (0.18ms, 30MB)
테스트 4 〉 통과 (0.57ms, 29.9MB)
테스트 5 〉 통과 (21.06ms, 34MB)
테스트 6 〉 통과 (6.63ms, 36.7MB)
테스트 7 〉 통과 (17.88ms, 37.1MB)
테스트 8 〉 통과 (43.71ms, 37.2MB)
테스트 9 〉 통과 (0.17ms, 30.1MB)
테스트 10 〉 통과 (3.16ms, 33.9MB)
테스트 11 〉 통과 (0.15ms, 30MB)
테스트 12 〉 통과 (27.54ms, 35.8MB)
테스트 13 〉 통과 (0.58ms, 29.9MB)
테스트 14 〉 통과 (0.30ms, 29.9MB)
테스트 15 〉 통과 (0.19ms, 30.1MB)
테스트 16 〉 통과 (0.19ms, 30.2MB)
테스트 17 〉 통과 (0.53ms, 29.9MB)
테스트 18 〉 통과 (0.16ms, 29.9MB)
테스트 19 〉 통과 (0.25ms, 29.8MB)
