프로그래머스 - Level2 N-Queen

문제 설명

문제 설명 생략

🙋‍♂️나의 풀이

🤔문제 접근

문제 해석

4 * 4 체스판에서 퀸을 (0, 0) 지점부터 놓고, 그 다음에 놓을 수 있는 자리를 계속 찾아나간다.

그림으로 표현하면 다음과 같다.

현재 행에 퀸을 놓으면 현재 행에는 더 이상 퀸을 놓을 수 없으므로 다음 행에 퀸을 놓을 수 있는지 검사해나간다.

기본 아이디어

더 이상 퀸을 놓을 수 없으면 이전으로 다시 되돌아가므로 백트래킹을 이용할 수 있다.

2차원 배열 상의 퀸의 위치를 저장하기 위해 1차원 배열을 사용했다.

그림으로 표현하면 다음과 같다.

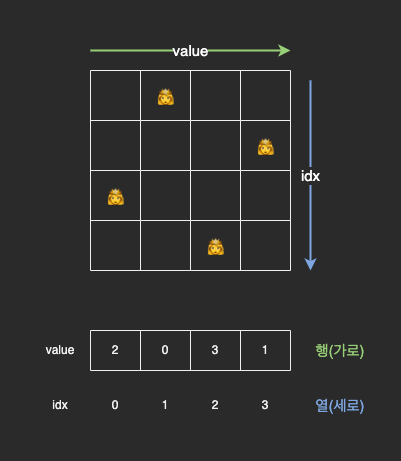
1차원 배열의 인덱스는 열, 해당 인덱스에 저장되는 값은 행으로 저장한다.

예를 들어, (0, 1) 에 위치한 퀸은 1차원 배열의 1번 인덱스에 0으로 저장되는 것이다.

즉, 행에 해당하는 정보는 위에서부터 몇 번째 가로 줄인지, 열에 해당하는 정보는 왼쪽에서부터 몇 번째 세로 줄인지 저장하는 것이다.

퀸을 놓을 수 있는 지 확인하기

체스판에서 놓을 수 있는 퀸의 위치를 확인하기 위해서는 2차원 배열이 아닌 1차원 배열에서 확인하면 된다.

확인해야 하는 것은 크게 3가지이다.

1. 가로에 퀸이 놓여져 있는가?
2. 세로에 퀸이 놓여져 있는가?
3. 대각선에 퀸이 놓여져 있는가?

우선 가로에 퀸이 놓여져 있는지 확인하기 위해서 1차원 배열에 같은 값이 있는 지 확인한다.

다음으로 세로에 퀸이 놓여져 있는지 확인하기 위해서 1차원 배열의 현재 인덱스에 값이 이미 존재하는 지 확인한다.

마지막으로 대각선 검사는 현재 놓으려는 위치와 1차원 배열에 저장된 값들을 비교한다. 정사각형에서 직선의 기울기가 1 또는 -1 이면 대각선이므로 이 성질을 이용해서 퀸이 놓여있는 지 확인할 수 있다.

직선의 기울기는 현재 위치의 세로 좌표 - 대상 위치의 세로 좌표 / 현재 위치의 가로 좌표 - 대상 위치의 가로 좌표 를 계산하면 얻을 수 있다.

✍️작성 코드

우선 체스판에 놓여진 퀸의 상태를 관리하기 위해 1차원 배열을 선언했다.

1
2

const NOT_VISITED = 100;
const status = Array(n).fill(NOT_VISITED);

NOT_VISITED 라는 상수를 선언해서 현재 열의 어느 행에도 퀸이 놓여지지 않았음을 표시한다.

다음으로 DFS 를 이용한 재귀 함수를 작성했다.

1
2
3
4
5
6
7
8
9
10
11
12
13

const dfs = (n, row, status) => {
  if (row === n) {
    answer += 1;
    return;
  }
  for (let col = 0; col < n; col++) {
    if (isAvailable(status, row, col)) {
      status[col] = row;
      dfs(n, row + 1, status);
      status[col] = NOT_VISITED;
    }
  }
};

재귀 함수의 종료 조건은 dfs 함수의 매개변수인 row 값(행)이 n 에 도달하면 종료하도록 설정했다. 0행부터 시작해서 n - 1 행까지 모두 퀸이 채워지면 가능한 경우의 수를 +1 해준다.

for 반복문 안에서는 현재 위치에 퀸을 놓을 수 있는지 확인한다. 만약, 퀸을 놓을 수 있으면 해당 자리에 row 값을 기록하고, dfs 함수에 row + 1 을 넘겨준다.

그리고 모든 탐색이 끝나고 다시 돌아나왔을 때, 현재 위치는 방문하지 않은 것(NOT_VISITED)으로 바꾸어 준다. 다음 열을 탐색할 때 이미 방문했던 경로를 방문하지 않아야 하기 때문이다.

현재 위치에 퀸을 놓을 수 있는 지 확인하는 함수 isAvailable 은 다음과 같다.

1
2
3
4
5
6
7
8
9

const isAvailable = (status, row, col) => {
  if (status[col] !== NOT_VISITED) return false;
  for (let idx = 0; idx < status.length; idx++) {
    if (Math.abs((row - status[idx]) / (col - idx)) === 1) {
      return false;
    }
  }
  return true;
};

1. 세로 검사
   • 1차원 배열 상에서 현재 접근한 인덱스(열)의 값이 비어있지 않다면, 즉 NOT_VISITED 가 아닌 다른 값이 있다면 이미 퀸이 놓였다는 의미이다.
2. 대각선 검사
   • 1차원 배열의 모든 값에 대해 현재 위치를 기준으로 기울기를 비교한다.
   • 직선의 기울기가 절댓값으로 1이면 대각선에 퀸이 놓여있다는 의미이다.

여기서 가로 검사는 하지 않았다.

dfs 함수를 보면 현재 위치에서 퀸을 놓을 수 있으면 다음 행을 검사하면 되기 때문에 row + 1 을 매개변수로 넘기고 있다. 즉, row 값은 이전 값이 저장되지 않으면 그 이상의 값은 저장되지 않기 때문에 별도로 가로 검사를 하지 않아도 되는 것이다.

전체 코드는 다음과 같다.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

function solution(n) {
  let answer = 0;
  const NOT_VISITED = 100;
  const status = Array(n).fill(NOT_VISITED);

  const isAvailable = (status, row, col) => {
    if (status[col] !== NOT_VISITED) return false;
    for (let idx = 0; idx < status.length; idx++) {
      if (Math.abs((row - status[idx]) / (col - idx)) === 1) {
        return false;
      }
    }
    return true;
  };

  const dfs = (n, row, status) => {
    if (row === n) {
      answer += 1;
      return;
    }
    for (let col = 0; col < n; col++) {
      if (isAvailable(status, row, col)) {
        status[col] = row;
        dfs(n, row + 1, status);
        status[col] = NOT_VISITED;
      }
    }
  };

  dfs(n, 0, status);

  return answer;
}

참고자료

• [백준] 9663번 - N-Queen [github.io]